Головоломка Овальный танграм

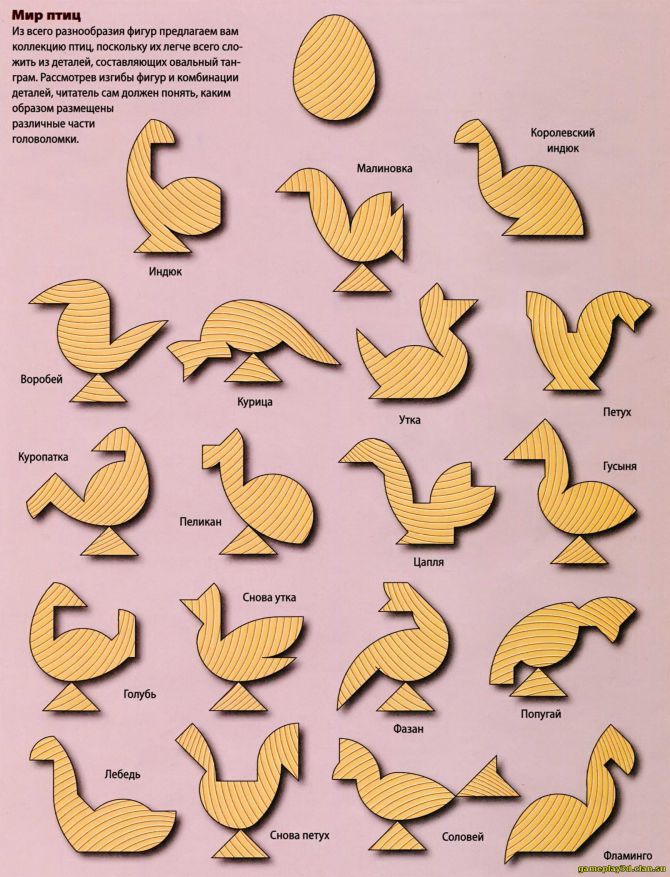
Овальный танграм

Что появилось раньше — яйцо или курица? В нашем случае ответ на этот вопрос очевиден. Конечно, яйцо! Из нашего чудо-яйца может появиться не только курица, но и индюк, малиновка, воробей, утка, фламинго... В общем, включаем фантазию, берем замечательную головоломку «Колумбово яйцо» и начинаем складывать причудливые фигурки. Кроме образцов, представленных здесь, вы наверняка соберете что-то новое и интересное!

Три детали с прямыми сторонами, как в классическом танграме, и шесть деталей-«гибридов» с прямыми и изогнутыми сторонами. Из этих элементов и состоит «Колумбово яйцо» —уникальный овал, из которого получается огромное количество интересных фигур.

Как и классический танграм, эта игра, также называемая «Волшебным яйцом», предлагает составить многочисленные фигуры всего лишь из девяти частей. Но, в отличие от обычного танграма, в ней есть изогнутые элементы, что добавляет фигурам интересные нюансы и делает их округлыми.

Длинная история

История этой игры берет начало в 1879 году, когда братья Отто и Густав Лилиенталь, инженеры и пионеры авиации, придумали способ ручного изготовления каменных блоков (названных камнями анкер) из кварцевого песка, гипса и льняного масла. Позже Фридрих Рихтер получил патент на эти блоки и в 1890 году начал производить из этого материала головоломки, состоящие из мелких деталей, формирующих разные фигуры. Одной из них и было «Колумбово яйцо», увидевшее свет в 1893 году. С помощью всего лишь девяти деталей из него можно было составить 95 различных фигур.

От Колумба до наших дней

Выражение «колумбово яйцо» обозначает задачу, на первый взгляд кажущуюся сложной, но на самом деле имеющую элементарное решение. Скорее всего, компания Рихтера вложила в новую головоломку именно такой смысл.

Один исторический анекдот разъясняет нам происхождение этого выражения. Говорят, что кардинал Педро Гонсалес Мендоса устроил банкет в честь Христофора Колумба, чтобы отметить его возвращение из первого путешествия в Америку. Во время ужина один из гостей имел неосторожность сказать вслух о том, что почитание Колумба безосновательно, поскольку такое путешествие могли бы проделать многие. Услышав это, Колумб пришел в ярость и предложил присутствующим поставить на стол яйцо вертикально. После долгих споров и высказывания различных версий Колумб слегка ударил яйцо о стол одной стороной — таким образом, чтобы скорлупа немного проломилась, — а затем без труда поставил его вертикально. Приглашенные начали возмущаться: якобы, любой мог сделать то же самое. На это Колумб ответил: многие задачи оказываются простыми, когда узнаешь их решение. Эта история стала настолько популярной, что в мире даже появилось несколько памятников «колумбову яйцу». Кроме того, существуют другие «колумбовы яйца» — фигуры овальной формы, способные стоять на вертикальной поверхности. Их придумал датчанин Пит Хейн, создатель таких известных игр, как «Геке» и «Кубики Сома». Его «суперяйца» — материализация уравнений, похожих на уравнения эллипсоида вращения. Но «суперяйцо», в отличие от «колумбова яйца», принимает вертикальное положение без использования уловок, а лишь потому, что кривизна его поверхности на вершинах равна нулю.

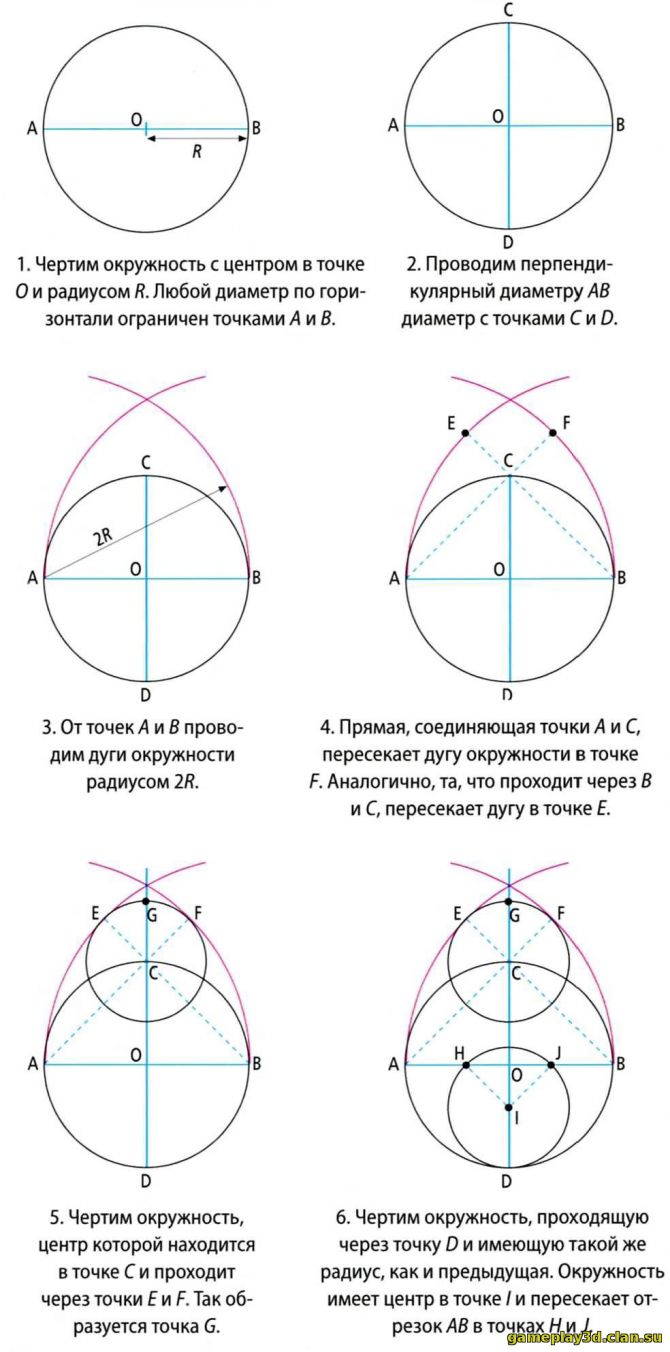
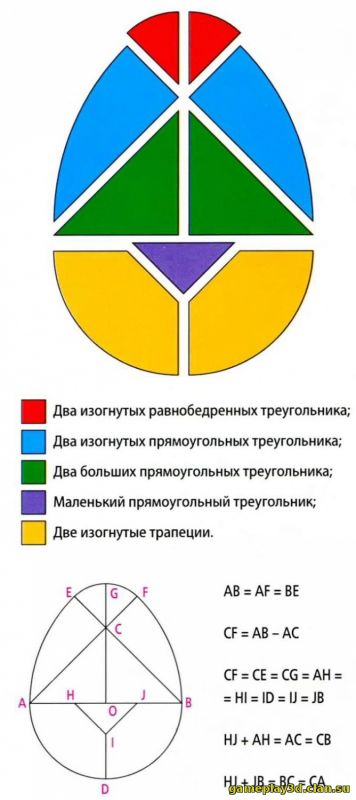
Конструкция овала

Девять деталей головоломки геометрически точно соотносятся между собой, поскольку они являются частью одного овала. Посмотрим, из каких геометрических фигур состоит овал и в какой последовательности появляются различные детали в процессе его образования. Наглядно продемонстрируем это.

Благодаря такому методу образования частей овала появляются следующие геометрические соотношения:

Существует разновидность «Колумбова яйца», где маленький прямоугольный треугольник разделен на две части. Естественно, при увеличении количества деталей головоломки расширяется диапазон возможных фигур.

Некоторые решения

Мы приводим лишь небольшое количество решений, чтобы читатель познакомился с деталями головоломки. Затем вы сможете самостоятельно создавать фигуры, дав волю своему воображению.