Игра Пятнашки

Будучи классической среди игр такого рода, эта головоломка занимает отдельное место в истории игр. А в свое время она привлекла к себе такой интерес общественности, что стала настоящим социальным «бедствием».

Пятнашки 16

Основной прием, используемый в этой головоломке, — механическое перемещение сегментов. Ее цель состоит в том, чтобы, передвигая помещенные в квадратную коробку пронумерованные фишки (но не вытаскивая их), расположить их по порядку номеров.

Наша игра предельно проста. Костяшки не могут быть извлечены, и единственное, что разрешено — это передвигать их внутри коробки. Естественно, передвигать их можно только на одну единственную свободную ячейку.

Сэм Лойд (1841—1911), великий популяризатор игры «Пятнашки 16», легенда развлекательной математики. Исключительно плодовитый автор, он создал огромное количество развлечений — от шахматных задач до различных игр и предметов, способных на невероятные превращения.

Великий выдумщик Сэм Лойд (1841 —1911) был главным изобретателем задач и загадок в истории США. Известный автор задач Мартин Гарднер описывал его так: «Высокий, худой, молчаливый индивидуалист, обладающий большими способностями к заклинаниям, пантомимам, чревовещанию, шахматам и быстрому вырезанию силуэтов из черной бумаги». Его страсть к шахматам, игре, в которую он начал играть в десять лет, не позволила ему блистать на турнирах, но сделала его очень популярным изобретателем оригинальных шахматных задач. В детстве он заинтересовался математическими загадками и изобретением удивительных и парадоксальных задач. Одна из самых известных — Trick Donkeys, или «Обманчивые ослики», которая была изобретена им еще в юношеские годы и вскоре принесла ему немалый доход.

Хотя «Пятнашки 16» и появились несколькими годами ранее, но настоящий успех пришел к ним только в 1878 году с легкой подачи Сэма Лойда — его «Головоломки 14—15» сразу же произвели фурор и стали известны за пределами страны. Говорят, что всюду можно было видеть людей, играющих в них: в поезде или в офисе (в рабочее время играть запретили), в Немецкой законодательной Ассамблее (в Рейхстаге) и в Париже, в городе и в деревне... Лойд предложил премию в тысячу долларов тому, кто сможет решить задачу «14—15». Многие говорили, что решили ее, но не могут вспомнить ходы. На самом деле у задачи не было решения, что было прекрасно известно Лойду. Именно по этой причине ему отказали в выдаче патента на изобретение. Однако игра существует и по сей день, и не только в нерешаемой версии, но и в комбинациях, которые решение имеют.

Знаменитые «Обманчивые ослики», одно из величайших изобретений Сэма Лойда. Необходимо заставить этих усталых осликов галопировать под всадниками, правильно скомбинировав все три картинки. Вы можете попробовать решить этот ребус, а можете посмотреть отгадку в конце статьи.

В чем заключается игра «Пятнашки 16» — неглубокая коробочка с шестнадцатью ячейками и пятнадцатью костяшками, пронумерованными от 1 до 15 в возрастающем порядке, слева-направо и сверху-вниз, и одна свободная ячейка, предназначенная для того, чтобы иметь возможность их передвигать (из игры изымается костяшка номер 16).

Необходимо нарушить порядок фишек и вернуть их в прежнюю позицию за наименьшее количество ходов. Идея «14—15» Сэма Лойда — не более чем еще один из вариантов игры: начав с основной позиции, надо поменять 14 и 15 местами, не нарушив при этом порядок остальных фишек, что является невозможным.

Некоторые версии игры не позволяют извлекать фишки из рамки, таким образом, всегда возможно вернуться на старую позицию (всего лишь проделав все ходы в обратном порядке). Но даже если мы и достанем костяшки — как в данном случае — и переложим их в произвольном порядке, у нас не будет никакой гарантии того, что в игре появится решение. Один из вариантов «Пятнашек» — игра с восьмью фишками, в которой мы можем играть во внутренней части, оставив недвижимыми костяшки на сером фоне. Есть вариант игры, где можно поменять порядок чисел от одного до восьми (так, чтобы порядок изменился с восьми до одного) в наименьшее количество ходов (можно достигнуть в 30 ходов).

---

Даже крестьяне прекращали работу, чтобы расставить 14 и 15 по своим местам. Так, на рисунке того времени изображены терзания крестьянина, пытающегося решить головоломку Сэма Лойда.

Игра с перемещениями

Давайте посмотрим, какая самая простая последовательность движений не изменяет расположение свободного места на игровой дощечке. Ограничимся группой из трех фишек и сформируем из них квадрат с одним свободным местом.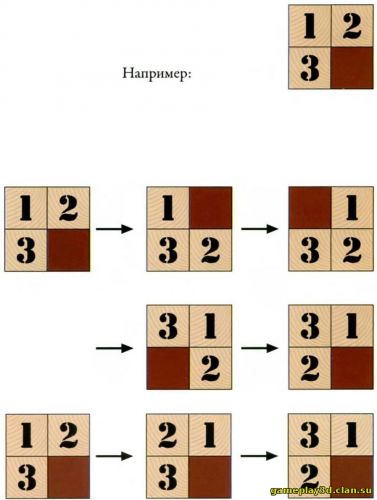

Меняя эти фишки местами, возвращаем свободное место на его изначальную позицию посредством следующих шагов:

Если мы позволим себе вытащить фишки из коробочки, то тот же результат может получиться при замене двух пар фишек. Первый шаг — это взаимозамена фишек 1 и 2, а затем — фишек 3 и 2:

Любая точная последовательность движений (при передвижении фишек) равносильна перестановке фишек (поднимая их), что в теории групп называется транспозицией. Представим как (а, b) транспозицию фишек а и Ь. Например, (1 2) (2 3) — последовательное применение двух предыдущих транспозиций. Так как самая простая последовательность взаимозаменяет две пары (это эквивалентно двум транспозициям), общее их количество всегда будет парным.

Это говорит о том, что если число транспозиций нечетно, то задача не имеет решения. Но решение негарантировано и в случае с четным количеством транспозиций. Без сомнения, хотя мы этого и не продемонстрировали, условия задачи также достаточно, чтобы убедиться в существовании ее решения.

Позиции, имеющие решения

Скажем, что позиция имеет решение, если от нее мы можем попасть на изначальную позицию или, что то же самое, от изначальной позиции обратно. Убедиться в том, что необходимое количество транспозиций парное или непарное, не всегда легко. Приведем еще один способ, чтобы определить, какие позиции имеют решение, что, кроме того, позволит нам еще раз бросить вызов Сэму Лойду. Первым делом надо заметить последовательность чисел, которая получается при пересечении поля способом, показанным на рисунке:

Таким образом, направление нашей цепочки следующее: 1—2—3—4—8—7—6—5—9—10— 11 — 12—15—14—13. Затем подсчитаем число последовательных перестановок, то есть сколько пар чисел расположено таким образом, что большее стоит перед меньшим. В случае с объективной последовательностью число 8 предшествует трем меньшим числам (7,6 и 5), число 7 — двум числам (6 и 5), число 6 — одному (5), 15 — двум (14 и 13) и 14 — одному (13). Следовательно, полное число перестановок равно 9. И, наконец, у нас есть критерий, позволяющий определить, какая позиция возможна для «Пятнашек 16»: Можно перейти с одной позиции на другую лишь в том случае, если число перестановок в обеих позициях имеет одинаковую четность, то есть либо они обе четные, либо обе нечетные. Так как это начальная позиция, то она имеет нечетное количество перестановок, то есть мы можем прийти к ней только с тех позиций, которые также имеют нечетное количество перестановок. Это объясняет, почему невозможно поменять 14 и 15, ведь в этом случае номер для перестановки четный. Действительно, перестановки одинаковы, как и в начальной позиции, кроме номеров 14— 15, а потому окончательное число перестановок равно восьми.

Простое доказательство

Мы увидим, что после любого движения количество перестановок продолжает быть четным или нечетным, в зависимости от того, какие действия привели к этому. Другими словами, мы покажем, что четность количества перестановок — это инвариант движения. Для начала убедимся в том, что боковое перемещение не изменяет перестановки, так как его движение ограничивается фишкой относительно пустого места, что не имеет воздействия на числовую цепь, которую мы строим. Теперь рассмотрим эффекты вертикального движения и проверим, что в этом случае сохраняется парность перестановок. В такой позиции:

перемещение вверх четверки заставит отстать четыре следующих позиции. Это происходит от 1—3—12—9—7—4—15—5... до 1—4—3— 12—9—7—15—5... Мы могли бы просчитать количество перестановок до и после передвижения, но удобнее считать, какие передвижения остались, а какие исчезли. Единственное новое перемещение — это 4—3, в то время как перемещения^—4, 9—4 и 7—4 уже не производятся. На самом деле все, что происходит теперь с четными фишками, — это то, что раньше было перестановкой еще до начала движения, а сейчас перестало ею быть, и наоборот. Являясь всеобщим, движение способствовало тому, чтобы стало на две перестановки меньше, таким образом, парность перестановок сохраняется. Относительно позиции пустого места может быть 0, 2, 4 или 6 фишек, на которые повлияло движение, то есть фишка, которая двигается, может обгонять и отставать на 0, 2, 4 или 6 мест. В любом случае, если это парное число, то разница в количестве перестановок между первоначальной и окончательной позициями должна обязательно быть парной.

Это решение знаменитой загадки Лойда об обманчивых осликах. Как вы можете видеть на изображении, разгадка этого ребуса Сэма Лойда достаточно проста и хитроумна.