Звездчатый ромбододекаэдр

Удивительный многогранник

Эта фигура на протяжении сотен лет привлекает к себе внимание зодчих и математиков — и не только своими необычными свойствами, но и эстетически безупречной формой.

Звездчатый ромбододекаэдр. Характерная для него схема заполнения пространства уникальна по своей красоте и изысканности.

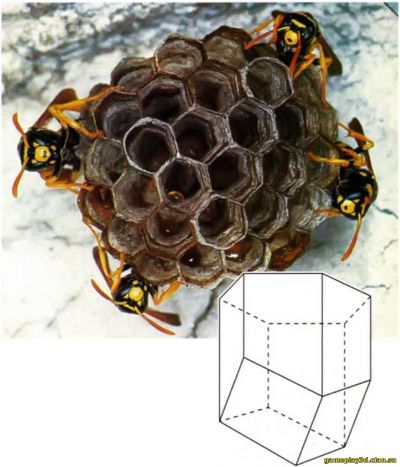
Первое формальное описание ромбододекаэдра дал немецкий астроном и математик Иоганн Кеплер (1571—1630 гг.). Он открыл его, изучая заинтересовавшее его строение ячеек пчелиных сот. Они имеют форму шестиугольной призмы, как бы оканчивающейся тремя условными «ромбами».

Почему пчелы предпочитают иметь дело именно с такими конструкциями? На протяжении всего XVIII в. ученые пытались ответить на этот вопрос.

Одно из тогдашних объяснений основывалось на том факте, что из всех фигур, полностью заполняющих пространство, подобные фигуры (при равном объеме) имеют наименьшую площадь. Получалось, что умные пчелы таким образом экономят воск, идущий на строительство сот.

Однако позднее выяснилось, что это утверждение было ошибочным. Нашлись другие способы завершения шестиугольной призмы, позволяющие сэкономить больше объема. Один из таких способов предоставляет усеченный восьмигранник. Другой вопрос — самый ли он экономичный? Многие исследователи до сих пор пытаются найти конечное решение этой проблемы, но пока безуспешно.

«Водопад» Морица Корнелиса Эшера. Славу этому художнику принесли работы, в которых «невозможное» творится в полном соответствии с математическими законами. На этой литографии водопад представляет собой вечный двигатель. Обратите внимание на многогранник, расположенный на вершине правой башни, — это звездчатый ромбододекаэдр.

Пчелиные соты принимают форму шестиугольной призмы, оканчивающейся тремя условными «ромбами». Взяв за основу эту структуру, можно построить двенадцатигранник, называемый ромбододекаэдром.

От классического ромбододекаэдра до многогранника Эшера

Из классического ромбододекаэдра легко построить звездчатый. Для этого следует «вытянуть» каждую из граней основной фигуры. При этом возможны различные варианты. Первый из получаемых звездчатых ромбододекаэдров как раз имеет форму нашей головоломки. Особенностью данной фигуры является возможность ее разделения на шесть равных частей. Задача состоит в том, чтобы сначала разъединить их, а затем вновь собрать воедино.

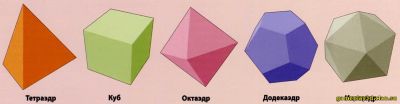
Что такое многогранник?

Многогранник — результат своеобразного логического (то есть проведенного по определенной схеме) «объединения» в пространстве нескольких плоских многоугольников (таких, как квадраты, треугольники и т. д.). Сами многоугольники при этом становятся гранями многогранника, а их стороны — его ребрами. Многогранник ограничен замкнутой поверхностью, то есть характеризуется объемом.

Самые известные тела этого ряда — так называемые выпуклые многогранники. Это такой многогранник, плоскости граней которого не «режут» его самого (его объема). По-другому, более наглядно, — если мы расположим одно из таких геометрических тел на столе, подложив под него лист бумаги (то есть совместив этот лист с одной из граней многогранника), то лист бумаги не будет «встречаться» (соприкасаться, пересекать) с другими его гранями.

Многогранник называется правильным, если: а) он является выпуклым; б) все его грани образованы правильными многоугольниками; в) в каждой вершине сходится одинаковое число граней; г) все его двухгранные углы равны.

Доказано, что существует всего пять правильных многогранников (по-другому их еще называют Платоновыми телами): это тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.

Свойства многогранника Эшера

Если мы возьмем несколько звездчатых ромбододекаэдров и попытаемся «прикладывать» их друг к другу, то очень скоро откроем самое замечательное свойство этого геометрического тела, а именно — его способность максимально «компактно» заполнять пространство. Иными словами, звездчатые ромбододекаэдры — абсолютно без зазоров — «складываются» в новый многогранник.

Можно доказать это свойство и чисто теоретически. Представим себе звездчатый ромбододекаэдр, вписанный в куб. Мысленно разделим куб на восемь равных частей, разрезав его двумя «перпендикулярными» плоскостями, проходящими через центр и параллельными граням куба. Одновременно на восемь равных частей делится и звездчатый ромбододекаэдр, причем объем каждой из них занимает ровно половину объема получившихся «кубиков». Другую половину полностью заполнит соответствующий фрагмент другого ромбододекаэдра (повторяющего первый), если мы приложим его сбоку.

Если звездчатый ромбододекаэдр вписать в куб, а затем разделить этот куб двумя «перпендикулярными» плоскостями, проходящими через его центр и параллельными граням куба, то в результате получится восемь равных «кубиков» (1), внутри каждого из которых находятся три пирамиды (2), в сумме занимающие ровно половину объема данного «кубика». Как показано на рисунке, эти пирамиды стыкуются без зазоров с тремя пирамидами такого же звездчатого ромбододекаэдра, располагаемого рядом (3).

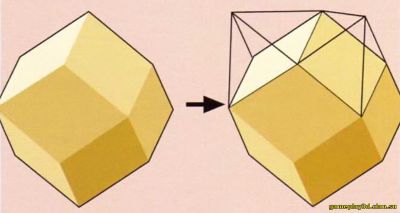
«Звездные» формы многоугольников и многогранников

Как получать из обычных многоугольников и многогранников звездчатые многоугольники и многогранники?

Простейший способ заключается в как бы «вытягивании» их сторон или граней. Но не произвольном «вытягивании» — оно совершается ровно по линиям прилегающих сторон или граней. Совсем просто это показать в двухмерном пространстве — на примере правильных многоугольников. Число сторон многоугольника при этом должно быть больше пяти. Если мы продлим стороны треугольника или квадрата, то эти линии не пересекутся, и никакого звездчатого многоугольника в результате мы не получим.

Первый такой многоугольник образуется при модернизации правильного пятиугольника. Это пятиконечная звезда (так называемая пентаграмма) — в нашем отечестве слишком хорошо всем знакомая. Впрочем, у пентаграммы очень долгая история, она служила магическим символом еще пифагорейцам.

Если мы распространим описанную процедуру на многогранники, то увидим, что «продлеваемые» грани, сходясь, образуют новую фигуру. Но, например, с подобным преобразованием куба нас постигнет неудача.

А вот правильный восьмигранник таким образом превращается в звездчатый октаэдр. Он был открыт еще Леонардо да Винчи, а спустя сто лет переоткрыт Кеплером, который назвал эту фигуру «восьмиугольной звездой». Ее можно рассматривать как соединение двух тетраэдров.

Продолжая стороны правильного пятиугольника, мы получим пятиконечную звезду — так называемую пентаграмму.

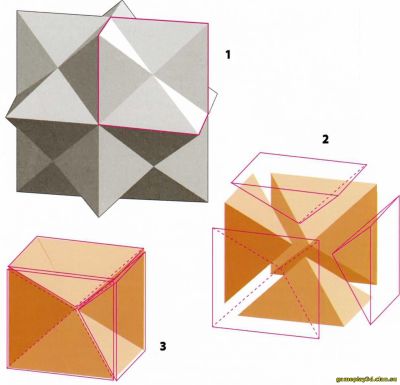
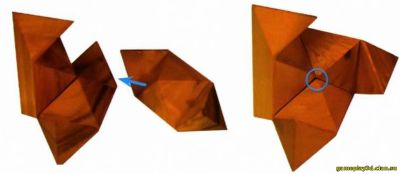
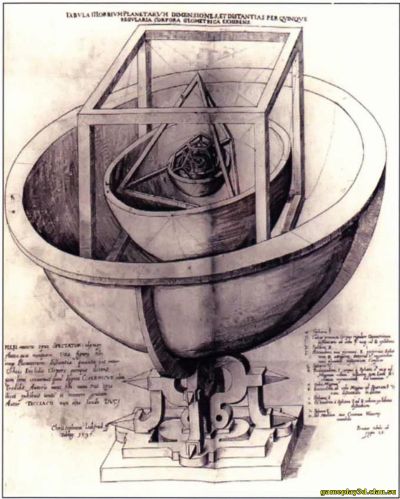
Правильные звездчатые многогранники 

Существует лишь четыре правильных звездчатых многогранника — математики их называют телами Кеплера-Пу-ансо. Два из них открыл Иоганн Кеплер (1571—1630 гг.) в начале XVII в., другие два — Луи Пуансо (1777—1859 гг.) в 1809 г. Их названия: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Первые три образованы на основе додекаэдра, а последний — на основе икосаэдра.

Чтобы получить малый звездчатый додекаэдр, нужно продолжить 12 граней правильного додекаэдра. Другие звездчатые многогранники получаются посредством несколько более сложных операций. Грани малого и большого звездчатого додекаэдра представляют собой пентаграммы, а грани звездчатого икосаэдра образованы 20 равносторонними треугольниками.

Вкупе с пятью Платоновыми телами, правильные звездчатые многогранники образуют «сообщество» правильных многогранников. Таким образом, их всего девять.

Отметим, что описанную процедуру «звездообразования» можно выполнять с любыми видами многогранников, повторяя ее сколько угодно раз. При этом получаются разнообразнейшие тела, обладающие немалыми художественными достоинствами.

Решение головоломки

Для начала убедитесь, что все представленные справа детали головоломки одинаковы. При попытке собрать звездчатый ром бододекаэдр оказывается несложным соединить первые пять деталей; проблема возникает с добавлением к конструкции последней детали.

Наилучший способ решения головоломки заключается в построении сначала двух фигур, каждая из которых состоит из трех деталей головоломки. Их собирают таким образом, чтобы средние точки полученных фрагментов можно было совместить.

 Обратите внимание, что ориентация полученных фигур разная.

На конец, берутся обе фигуры — по одной в каждую руку — и осторожно соединяются между собой. Теперь в руках у вас — звездчатый ромбододекаэдр собственной персоной.

Иоганн Кеплер придумал эту модель вписанных правильных многогранников, чтобы наглядно показать соотношение расстояний между планетами Солнечной системы. Внешняя сфера, описывающая куб, соответствует орбите Сатурна, а внутренняя, описывающая тетраэдр, — орбите Юпитера.